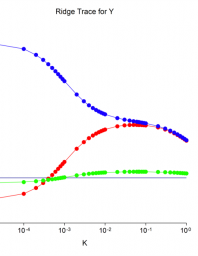
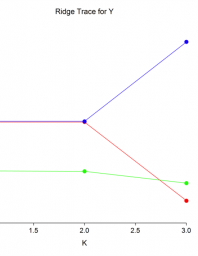
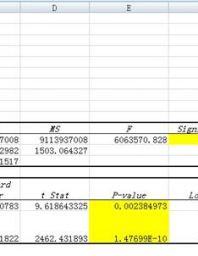
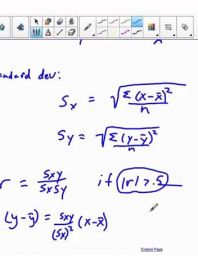Regression analysis is very much important for data mining.
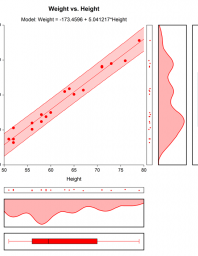
Used to measure the magnitude of the relationship between variables. Regression analysis can be performed using a single variable or multiple variables. In many cases, the other variables affecting the dependent variable are assumed to be fixed (in the form of Ceteris Paribus). It is determined by a coefficient that how these variables affect the dependent variable. This variable is called the regression coefficient of the variable and indicates the degree of dependence. What is important is that there is a causal relationship between the affected and the affected.
Where do you use the regression analysis?
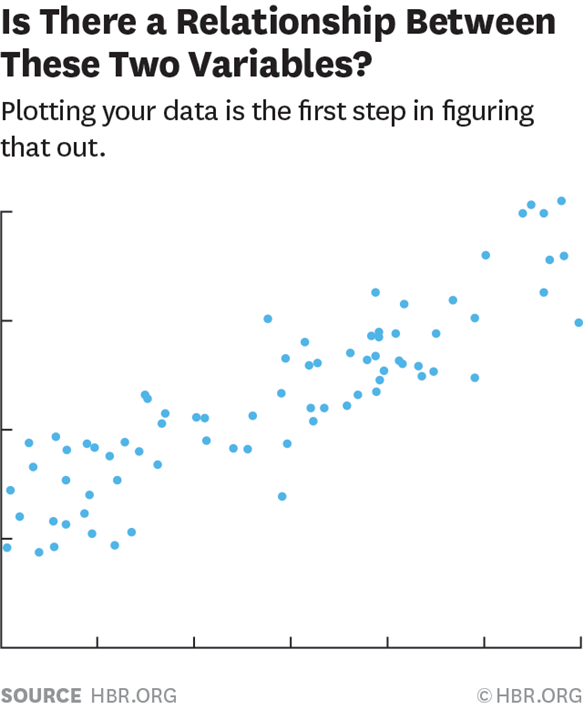
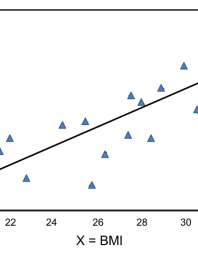
Regression analysis can be used to establish a link between the number of absences days and the grade of success for the student who will give an example between the time worked and the grade received or by taking the course out of education again. After quantifying the relation, the success status of a student who is known to be absent or the absentee status of a student whose achievement is known can be estimated. Of course, both measurements have to be quantitative measures.
Regression models: Simple Regression Model
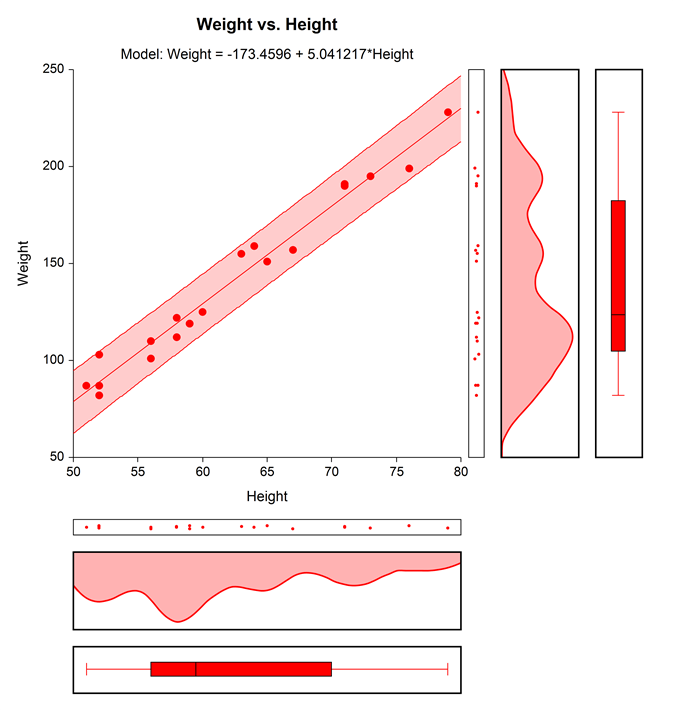
The most primitive and first use of the regression method is the least squares method. The least squares method was first put forward by the Parisian mathematician Adrien Marie Legendre in 1805.
The smallest squares method we think belongs to Gauss is due to its attractive team statistical properties. Is a widely used method in regression studies. The method is used to identify relationships between variables in various branches of science such as medicine, finance.
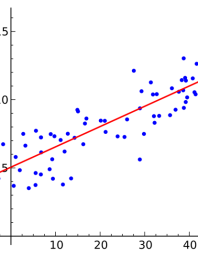
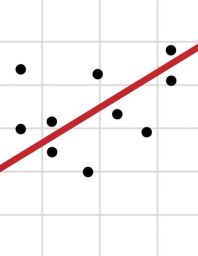
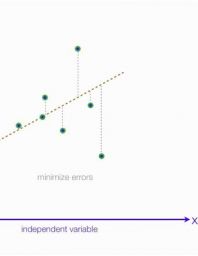
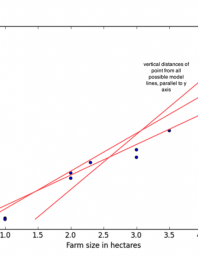
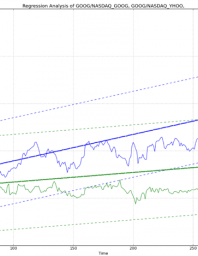
The deviations of the coefficients that produce close results will be as in the graph above. In the least squares method, the coefficients of the least squares of these deviations are chosen as the solution. You can examine the Least Squares calculation method file for calculation details of the equation making the best guess .
We can Minimize Bug Totals.
İn the regression analysis, even for very high error values where positive and negative values will swallow each other, meaningless results such as 0 errors in total will be produced. Although there are fewer errors in the graph on the left, we will see that the error on the right is less accurate when we minimize the error totals. For this reason, this method is far from practical. In this case, a situation like the one below is encountered. Here, the second graphic seems to give a better guess than the first graphic. Error Frames Total Can Be Minimized . This method is called the Least Squares method. The advantages of the method are: Taking square sums of mistakes removes the sign problem. Since the square is taken, the bigger ones are multiplied twice and the emphasis is increased. All points and mistakes.